Wenhu Wang,Hibba Arshad,Asfand Fahad,⋆and Imran Javaid

1School of Software,Pingdingshan University,Pingdingshan,China

2College of Computing and Information Technologies,National University,Manila,Philippines

3Henan International Joint Laboratory for Multidimensional Topology and Carcinogenic Characteristics Analysis of Atmospheric Particulate Matter PM2.5,Pingdingshan,China

4Centre for Advanced Studies in Pure and Applied Mathematics,Bahauddin Zakariya University,Multan,Pakistan

ABSTRACT One of the most recent developments in the field of graph theory is the analysis of networks such as Butterfly networks,Benes networks,Interconnection networks,and David-derived networks using graph theoretic parameters.The topological indices(TIs)have been widely used as graph invariants among various graph theoretic tools.Quantitative structure activity relationships(QSAR)and quantitative structure property relationships(QSPR)need the use of TIs.Different structure-based parameters,such as the degree and distance of vertices in graphs,contribute to the determination of the values of TIs.Among other recently introduced novelties,the classes of ev-degree and ve-degree dependent TIs have been extensively explored for various graph families.The current research focuses on the development of formulae for different ev-degree and ve-degree dependent TIs for s−dimensional Benes network and certain networks derived from it.In the end,a comparison between the values of the TIs for these networks has been presented through graphical tools.

KEYWORDS Topological indices;ev-degree;ve-degree;butterfly network;benes network

A classic and helpful strategy is to attach various graphs to objects that may be an algebraic structure,a chemical structure of a drug,or a network,which assists in understanding certain features of the objects.Various graph parameters can be associated with the properties of the structure under examination which leads to a deeper study of its theory.These properties may include the algebraic properties of the zero divisor graphs and the physio chemical properties of the chemical structures.By adopting this strategy,several researchers studied different objects such as algebraic objects [1],pysio-chemical properties of chemical structures[2–4],drugs used for breast cancer treatment[5],and interconnection networks[6].The analysis of networks,such as Butterfly network[7],Benes network[8,9],Interconnection network[6,10]and David-derived network[11]through similar approach,is one of the most recent developments in the field of graph theory.

The class of topological indices(TIs)is a significant class of parameters associated with graphs.Many TIs have been introduced and studied during the last fifty years.Among the class of degree dependent TIs,the Zagreb indices(ZIs)introduced in[12],vastly studied due to the ability to estimate theπ-electron energy is still a topic of interest[13]after 5 decades.Another degree dependent graph parameter,used in mathematical chemistry is known as Randíc index(RI).The details regarding its applications and its different variants are presented in [14].Furthermore,the geometric-arithmetic(GA)index was formulated[15]in an attempt to exceed the Randíc index in terms of predicting ability.Its chemical use and mathematical characteristics drew scientists to examine it further in[16].Another significant index,known as Atom bond connectivity index(ABC-index)was put forward by Estrada and was used for investigating stain energy and stability of cycloalkanes and linear alkanes,see[17–20].Another graph invariant,having connections with eigen values of graphs was introduced in[21]and is a topic of interest till now known as Harmonic index(HI).In[22],Chellali et al.introduced some new degrees of a vertex in a graph,known as ve-degree and ev-degree.Mathematical notions related to these degrees were also studied by Horoldagva et al.[23].The ZIs and RI,based on ev-degree and ve-degree notions,are formulated in[24–27]and it was analyzed that predicting ability of ve-degree ZI has improved as compared to its classical version.For more developments on the study of TIs,see[28–32].

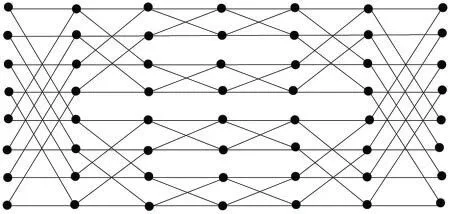
Figure 1:3-dimentional Benes network

Butterfly graphs are the associated graphs of Fast Fourier Transforms (FFT) networks which are especially effective in performing the FFT.The butterfly network is constructed by a sequence of switch stages and connector patterns that allow′n′different configurations.The′n′outputs should be connected to′n′inputs.Furthermore,the Benes network obtained by attaching back-toback butterfly networks is known for permutation routing [8].These networks are key multistage interconnection networks with appealing communication network topologies[9].The graph associated tos-dimensional butterfly network consists of vertex setVwith elements [v,i] in whichvis ans-bit binary number representing the row of the node and 0≤i≤s.The edge between any two vertices[v,i]and[v′,i′]exists if and only ifi′=i+1 and either(1)v=v′or(2)v,v′differ in exactly theith bit.Clearly,for|V(BF(s))|=2s(s+1)and|E(BF(s))|=s2s+1.Further,ansdimensional Benes network is obtained by connecting back-to-back butterfliesBF(s).Ans-dimensional Benes network is denoted byB(s),for exampleB(3)is shown in Fig.1.Further,|V(B(s))|=2s(2s+1)and|E(B(s))|=s2s+2.For more regarding the structure and construction of butterfly and benes networks,we refer readers to[6].By keeping in view the importance of these networks,Hussain et al.recently introduced some families of graphs obtained by Horizontal and vertical identifications of Benes network.These new graphs are known as Horizontal Cylindrical(HCB(s))and Vertical Cylindrical(VCB(s))Benes network.In these networks,|V(HCB(s))|=(2s−1)(2s+1),|V(VCB(s))|=2s+1s,|E(HCB(s))|=2s(2s+1−1) and|E(VCB(s))|=2s+2s.For the complete details regarding the structuresHCB(s)andVCB(s),see Figs.2 and 3[33,34].

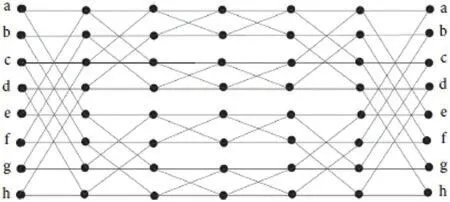
Figure 2:Normal representation of VCB(3)

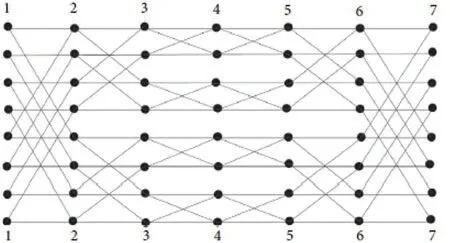
Figure 3:Normal representation of HCB(3)

LetG(V,E)denotes a connected graph havingVas a vertex set andEas an edge set.Foru∈V,the degreeu,denoted byd(u)is the cardinality of edges incident to it.For anyu,v∈V,the verticesu,vare called adjacent if there ise∈Ewithe=uv.Foru∈Vits open neighborhood,denoted byN(u),is defined as:N(u)={v∈V:there exists e∈E with e=uv} and the closed neighborhoodN[u]={u}∪N(u).Foruv=e∈E,its ev-degree is the cardinality of the vertices inN[u]∪N[v]and the ve-degree ofv∈Vis the cardinality ofN[v].The ev-degree ofeand ve-degree ofuare denoted bydev(e)anddve(u),respectively.In Table 1,we include the formulae of ev-degree and ve-degree dependent variants of the well known TIs discussed above.

Table 1: Ev-degree and ve-degree based TIs of a Graph G(V,E)

Table 1 (continued)2 (G)=Σ uv∈E(G)(dve(u)dve(v))RI(VE)Rve(G)=Σ uv∈E(G)((dve(ut)dve(v)))−1/2 2nd ZI(VE)Mveimages/BZ_869_1645_737_1683_783.pngABC-I(VE)ABCve(Gt)=Σ dve(u)+dve(v)−2 dve(u)dve(v)GA-I(VE)GAve(G)=Σ uv∈E(G)2√dve(u)dve(v)dve(u)+dve(v)HI(VE)Hve(G)=Σ uv∈E(G)2 dve(u)+dve(v)Sum-Connectivity Index(VE)χve(G)=Σ uv∈E(G)(dve(u)+dve(v))−1/2 uv∈E(G)

In this section,we prove analytical formulae for the ev-degree dependent TIs forB(s),VCB(s)andHCB(s).The formulae have been established through partition of the vertex sets ofB(s),VCB(s)andHCB(s)on the basis of ev-degree as shown in Tables 2–4.We start with the following theorem forB(s).

Table 2: Ev-degree based partition of V(B(s))

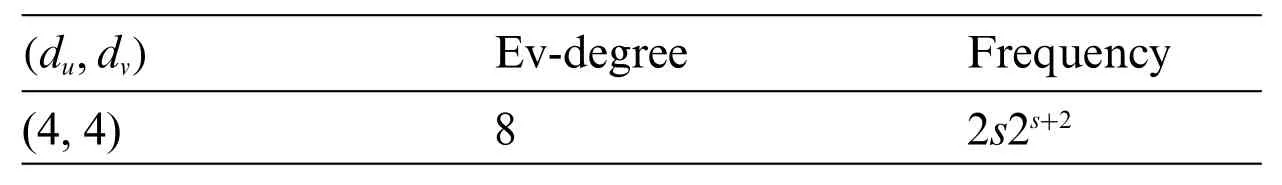
Table 3: Ev-degree based partition of V(VCB(s))

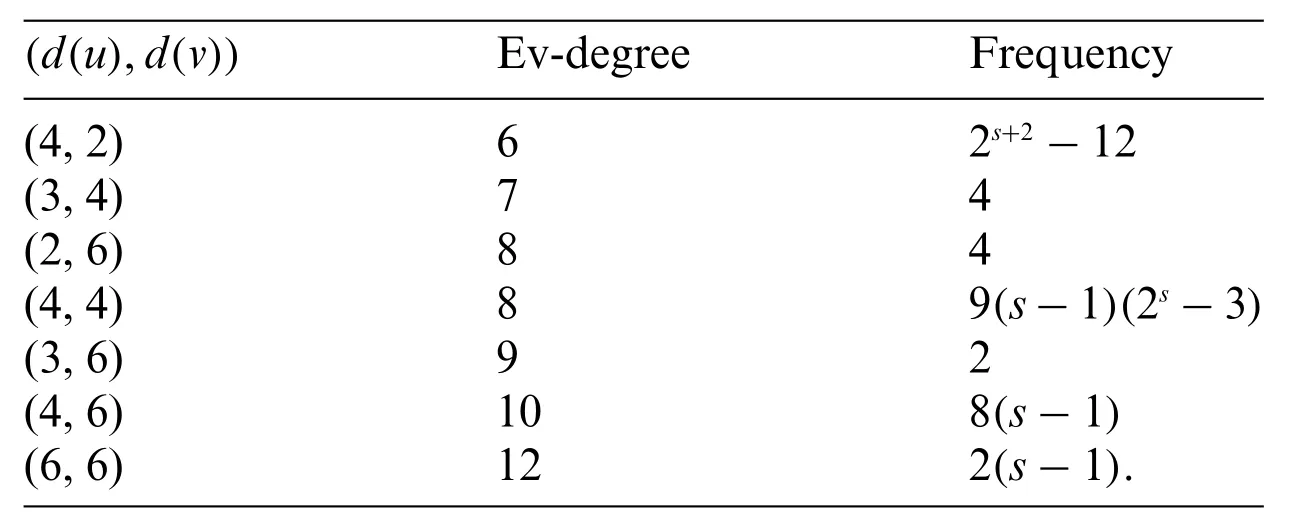
Table 4: Ev-degree based partition of V(HCB(s))

Theorem 3.1.For ans-dimensional Benes networkB(s),we have:

(i)Mev(B(s))=2s+2(64s−28).

(ii)Rev(B(s))=

Proof.

By using Table 2,we compute the ev-degree based indices for Benes network as follows:

Now,we continue to prove the ev-degree dependent TIs forVCB(s)in the next theorem.

Theorem 3.2.ForVCB(s),theMev(VCB(s))andRev(VCB(s))are given as:

(i)Mev(VCB(s))=2s+9·s.

(ii)Rev(VCB(s))=

Proof.(i)From Table 3 and the definition ofMev,we have:

(ii)From Table 3 and the definition ofRev,we have:

We conclude the results of this section by proving the ev-degree dependent TIs forHCB(s):

Theorem 3.3.ForHCB(s),theMev(HCB(s))andRev(HCB(s))are given as:

(i)Mev(HCB(s))=2s+7(2s−1)+320s−138.

(ii)Rev(HCB(s))=

Proof.(i)From Table 4 and the definition ofMev,we have:

which upon simplification gives the required result.

(ii)From Table 4 and the definition ofRev,we have:

which upon simplification gives the required result.

Now,we present an example of the results proved in this section:

Example 3.1.By takings=4 in Theorem 3.1,Theorem 3.2 and Theorem 3.3,we obtain the values of ev-degree based TIs forB(4),VCB(4)andHCB(4)as shown in Table 5:

Table 5: Ev-degree based TIs for B(4),VCB(4)and HCB(4)

In this section,we develop formulae for the ve-degree dependent TIs forB(s),VCB(s)andHCB(s).The key to obtaining these formulae is to obtain partition the edge set ofB(s),VCB(s)andHCB(s)on the basis of ve-degrees of the end vertices of each edge as shown in Tables 6–8.

Table 6: Partition the edge set of B(s)in terms of ve-degrees of end vertices

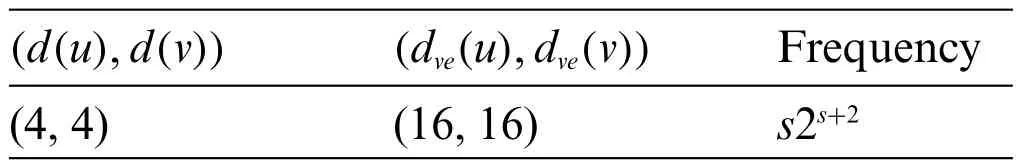
Table 7: Partition the edge set of VCB(s)in terms of ve-degrees of end vertices

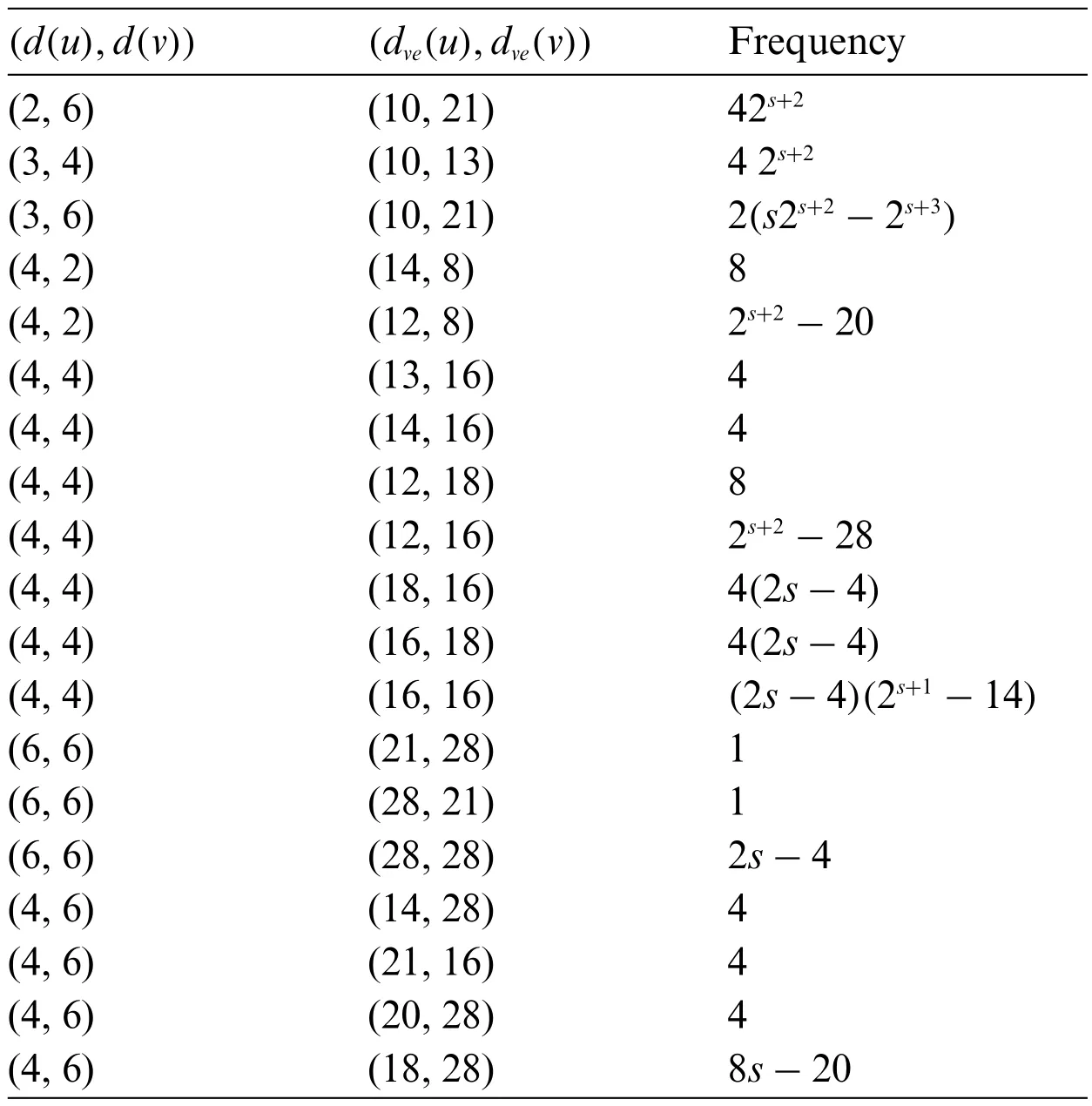
Table 8: Partition the edge set of HCB(s)in terms of ve-degrees of end vertices

Theorem 4.1.ForB(s),the ve-degree dependent TIsM1α ve(B(s)),M1β ve(B(s)),M2v e(B(s)),Rve(B(s)),ABCve(B(s)),GAve(B(s)),Hve(B(s))andχve(B(s))are given as:

Proof.(i)From Table 6 and the definition ofM1αve,we have:

which upon simplification gives the required formula.

(ii)The Table 6 and the formula forM1βveyields:

(iii)The Table 6 and the formula forM2veyields:

(iv)The Table 6 and the formula forRvegives:

(v)The Table 6 and the formula forABCveyields:

(vi)The Table 6 and the formula forGAveyields:

(vii)The Table 6 and the formula forHveyields:

(viii)Lastly,the Table 6 and the formula forχvegives:

which upon simplification gives the required formula.

By using the Table 7 and the formulae of TIs defined in Table 1,we get the following results for theVCB(s).

Theorem 4.2.ForVCB(s),ve-degree dependent TIsM1α ve(B(s)),M1β ve(B(s)),M2v e(B(s)),Rve(B(s)),ABCve(B(s)),GAve(B(s)),Hve(B(s))andχve(B(s))are given as:

By using the Table 8 and the formulae of TIs defined in Table 1,we get the following results for theHCB(s).

Theorem 4.3.ForHCB(s),the ve-degree dependent TIsM1α ve(B(s)),M1β ve(B(s)),M2v e(B(s)) andRve(B(s))are given as:

Now,we conclude the section by including the following example:

Example 4.1.By takings=4 in Theorem 4.1,Theorem 4.2 and Theorem 4.3,we obtain the values of ve-degree based TIs forB(4),VCB(4)andHCB(4)as shown in Table 9:

Table 9: Ve-degree based TIs for B(4),VCB(4)and HCB(4)

We proceed further with our obtained formulae in previous section to study graphical patterns in the values of TIs ofB(s),HCB(s) andHCB(s).In Figs.4–6,the patterns of ZI(VE),RI(VE),ABCI(VE),GA-(VE) and HI(VE) (on y-axis),where the value ofshas been taken on x-axis,forB(s),HCB(s) andVCB(s) have been presented.All the figures show the rapid rise in the values of each TI forB(s),HCB(s) andHCB(s) with the rise in the value ofs.The trends in Fig.4 (L) show that theHCB(s) attains higher values of ZI(VE),whereas values of ZI(VE) forVCB(s) remain betweenB(s)andHCB(s).Similar trend for RI(VE)has been shown in Fig.4(R).In Fig.5(L),it can be seen that the values of ABC-I(VE)show different behaviours as in case of ZI(VE)and RI(VE).The ABCI(VE)attains lowest values forHCB(s),whereas values forB(s)remain betweenVCB(s)andHCB(s).Furthermore,the trend for HI(EV)is shown in Fig.5(R).In the case of GA(VE),the values forB(s)remain the highest and the values forVCB(s)remain between the values ofB(s)andHCB(s),see Fig.6.

Figure 4:Graphical comparison between ZI(VE)on left(L)and RI(VE)on right(R)of B(s),HCB(s)and HCB(s)

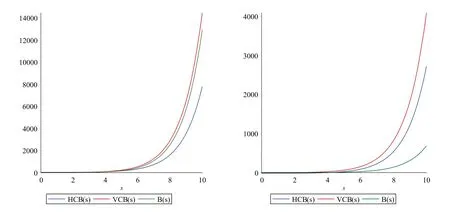
Figure 5: Graphical comparison between ABC(VE) on left (L) and HI(VE) on right (R) of B(s),HCB(s)and HCB(s)

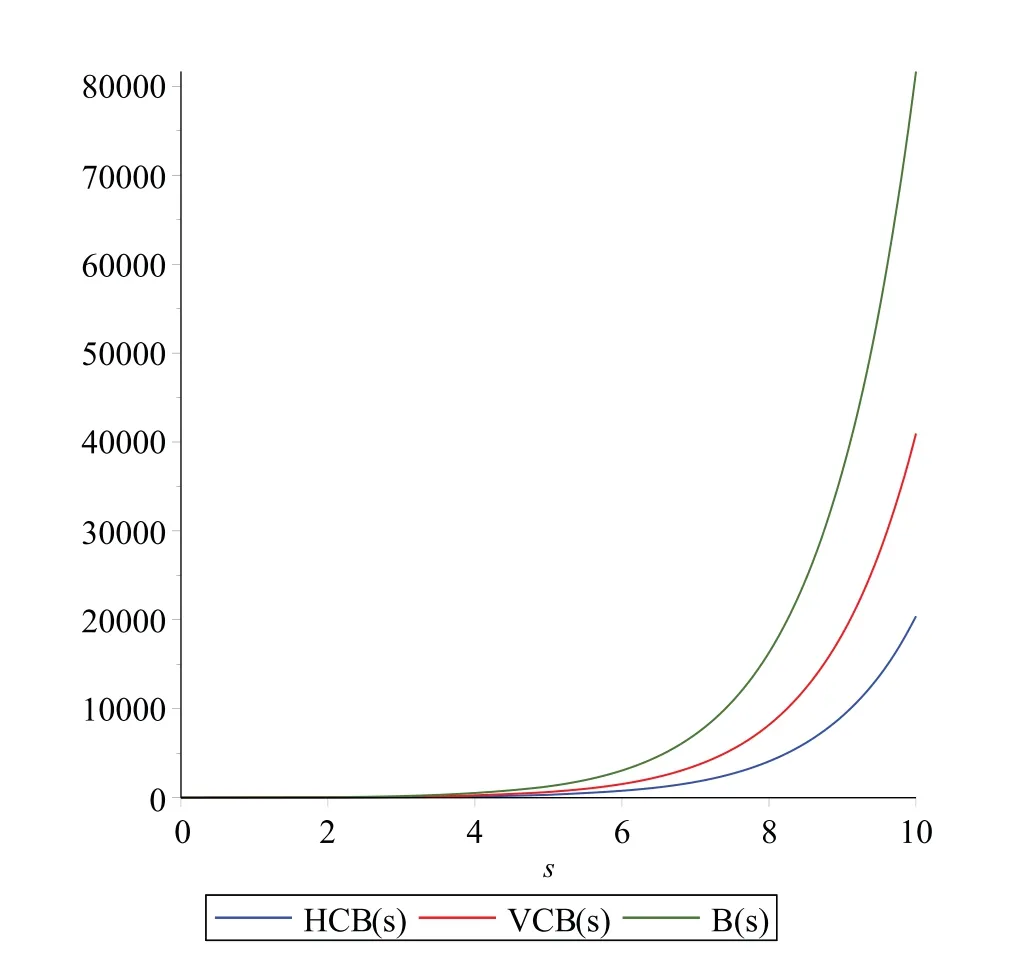
Figure 6:Graphical comparison between GA-I(VE)of B(s),HCB(s)and HCB(s)

The study of newly formed networks is always a fascinating topic.UsingB(s),several novel networks such asHCB(s) andVCB(s) have been defined through identifications in [33] and further investigated in [34].Furthermore,the ev-degree and the ve-degree of these structures were not investigated yet.In the current work,we constructed the ev-degree based partition of the vertex set and the ve-degree based partition of the edge set for these networks.Through these partitions,we developed formulae for several ev-degree and ve-degree based TIs forB(s),HCB(s) andVCB(s) in terms of the parameters.Further,we presented the comparative analysis of the values of ZI(VE),RI(VE),ABC-I(VE),GA-I(VE)and HI(VE)forB(s),HCB(s)andVCB(s).It is observed that similar patterns have been developed for ZI(VE)and RI(VE),whereas the other three TIs produce different trends.

Acknowledgement: The authors are thankful to their respective institutes.

Funding Statement: This work is partially supported by the National Natural Science Foundation of China(Grant No.61702291);China Henan International Joint Laboratory for Multidimensional Topology and Carcinogenic Characteristics Analysis of Atmospheric Particulate Matter PM2.5.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.