郭艺杰

⦿福建省漳州第一外国学校

近几年来，函数同构问题经常在高考试题中出现，利用同构式解决函数问题往往能起到事半功倍的效果，但也需要学生具备较强的直观想象、逻辑推理等数学素养.如何分辨一个问题是否为同构问题，以及如何构造同构式是这类问题的难点.本文中以历年高考中的同构问题为例，探索解决此类问题的应对策略，供读者参考.

(1)同构式指的是函数解析式相同，只有变量不同的式子.

(2)同构中经常用到的函数及其极值点：

y=lnx-x，极大值点为1；

y=ex-x，极小值点为0；

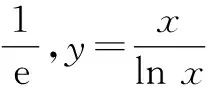
(3)同构问题常用到的恒等变换：

(4)同构中常用放缩法：

指数放缩：ex≥x+1(x=0时等号成立)；
ex≥ex(x=1时等号成立).

例1(2020全国1卷理科·12)若2a+log2a=4b+2log4b则( ).

A.a>2bB.a<2b

C.a>b2D.a

解析：考虑到等式左边2a+log2a不容易化简，因此对等式右边4b+2log4b=22b+log2b进行转化，发现左右两边形式上相近，但又不完全相同，因此右式作拼凑右式=22b+log2b+1-1=22b+log2(2b)-1=左式，发现22b+log2(2b)>2a+log2a，考虑到不等式左右两边同构.令f(x)=2x+log2x有其在定义域上单调增，且由同构有f(2b)>f(a)，所以2b>a.故选择：B.

点评：当一个等式里面含有两个未知量，且形式上相近，可以考虑利用恒等变换转化成同构式，并利用函数的增减性进行判断、证明.

同类型推广：若a+lna=2b+lnb，求a的范围.

分析：2b+ln 2b>2b+lnb=a+lna>b+lnb，所以有2b>a>b.

例2(2020新高考Ⅰ卷·21)已知函数f(x)=aex-1-lnx+lna.(1)略；
(2)若f(x)≥1，求a的取值范围.

分析：恒等变换f(x)=aex-1-lnx+lna=ex-1+ln a-lnx+lna≥1，考虑把ex-1+ln a的指数当成整体变量，所以拼凑出ex-1+ln a+(x-1+lna)≥x+lnx=eln x+lnx，可以看出左右同构.令g(x)=ex+x，知其单调递增且有g(x-1+lna)≥g(lnx)，可以得到x-1+lna≥lnx，所以lna≥-(x-1-lnx)，又因为右式的最大值为0，所以得到a≥1.

点评：构造同构式的时候经常利用指数与对数的恒等变换，把“谁”看成整体变量关乎同构式能否构造成功.

点评：在构造同构式的时候，通常要先把某个变量或是参数分离到等式或不等式的一边，而且同一个题目可能有多个同构方式，选择合适的同构式，可以使解题更加便捷.

例3(2022新高考Ⅰ卷·22)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.

(Ⅰ)求a；

(Ⅱ)证明：存在y=b，其与两条曲线y=f(x)和y=g(x)共有三个不同的交点，并且从左往右三个交点的横坐标成等差数列.

解析：(Ⅰ)易求得a=1.

(Ⅱ)同构式法.

由(Ⅰ)可知f(x)=ex-x,g(x)=x-lnx，所以由f′(x)=ex-1，知在(-∞,0)上f(x)单调递减，在(0,+∞)时f(x)单调递增.又有x→-∞时，f(x)→+∞；
所以f(x)min=f(0)=1.

所以存在y=b与两条曲线y=f(x)和y=g(x)共有三个不同的交点，设交点横坐标为x1<0

f(x1)=ex1-x1=f(x2)=ex2-x2=b，

b=g(x2)=x2-lnx2=g(x3)=x3-lnx3.

由恒等变换可得x2-lnx2=eln x2-lnx2,x3-lnx3=eln x3-lnx3.

所以g(x2)=f(lnx2),g(x3)=f(lnx3).所以有f(x1)=f(x2)=f(lnx2)=f(lnx3).

又因为x1<0

f(x1)=x2-x1,f(x2)=x3-x2.

所以x2-x1=x3-x2.

点评：第(Ⅱ)问的证明，利用同构式来解决，大大简化了标准答案的分析讨论过程，简单明了、事半功倍，也更容易让学生接受.

在利用同构式解决函数问题时，首先应该考虑哪些情况下可同构.常见的有f(a)=f(b)，f(a)>f(b)，f(a)

同构问题作为这几年高考的常考题型，经常用于考查不等式的证明或求解，经常以关于ex与lnx的函数问题为背景.在构造同构式的时候，由于技巧性较强，需要学生具备较强的推理能力和分析能力.而利用同构式解决小题时，常常又能起到意想不到的效果；
而且对于大题的证明和求解，同构法可以使过程更加简洁，更便于学生理解.因此在平常的教学中对于此类问题，多加练习、研究、巩固形成模式还是相当必要的.

猜你喜欢同构等式交点巧用同构法解决压轴题中学生数理化(高中版.高二数学)(2022年6期)2022-06-30指对同构法巧妙处理导数题中学生数理化(高中版.高二数学)(2021年2期)2021-03-19同构式——解决ex、ln x混合型试题最高效的工具中学生数理化(高中版.高二数学)(2021年2期)2021-03-19高等代数教学中关于同构的注记高师理科学刊(2020年2期)2020-11-26组成等式数学小灵通(1-2年级)(2020年9期)2020-10-27阅读理解学生导报·东方少年(2019年7期)2019-06-11一个连等式与两个不等式链新高考·高一数学(2018年5期)2018-11-22借助函数图像讨论含参数方程解的情况数学学习与研究(2017年11期)2017-06-20试析高中数学中椭圆与双曲线交点的问题青年时代(2017年3期)2017-02-17一个等式的应用考试周刊(2015年105期)2015-09-10