胡芯忆, 何德彪, 彭 聪, 罗 敏, 黄欣沂

1. 武汉大学 国家网络安全学院 空天信息安全与可信计算教育部重点实验室, 武汉 430072

2. 香港科技大学(广州) 信息枢纽 人工智能学域, 广州 511455

基于身份的密码体制(identity-based cryptography, IBC) 由Shamir[1]于1984 年提出, 其思想是将用户的身份信息作为公钥, 由可信的密钥生成中心(key generation center, KGC) 为每个用户生成其身份信息对应的私钥, 这种方式无需使用公钥证书来证明用户身份与用户公钥的绑定关系, 简化了公钥基础设施(public key infrastructure, PKI) 中用户公钥证书的管理. 2016 年3 月, 国家密码管理局发布行业标准“GM/T 0044-2016《SM9 标识密码算法》”, 包括总则、数字签名算法、密钥交换协议、密钥封装机制和公钥加密算法、参数定义五个部分[2]. 成为国家标准以后, SM9 算法在各行业领域的应用更加广泛. 双线性对是SM9 密码算法的核心运算部件, 它的性能决定了SM9 密码算法的性能. 研究双线性对的高效实现对推动SM9 算法的应用和落地具有重要的价值.

常见的双线性映射主要有Weil 对[3]和Tate 对[4]. 双线性对可以通过Miller 算法[5]有效计算.研究发现Tate 对在计算效率方面优于Weil 对[6,7], 因此Tate 对一直是研究关注的重点. 后来, 学者们相继提出了Tate 对的变体, 如Ate 对[8]、O-ate 对[9]和R-ate 对[10]等, 这些双线性对有效降低了Miller 算法的迭代次数, 减少了计算量, 计算效率更高. Barreto 等人[11]提出了Tate 对新的定义公式, 减少了Miller 算法中的无关运算, 避免了扩域中的求逆运算. Barreto 和Naehrig 提出了一族配对友好(pairing-friendly) 的素数阶椭圆曲线, 嵌入度为12, 其定义为E:y2=x3+b,b/= 0, 这类曲线统称为Barreto-Naehrig 曲线, 即BN 曲线[12], 可以有效降低Miller 算法的迭代次数. Scott 等人[13]利用非超奇异椭圆曲线上的有效自同态, 通过计算Miller 算法的中间值减少Tate 对的计算量. Galbraith等人[14]在大素数特征域上的一大类椭圆曲线上构造了一种可计算的有效自同态, 可用于加速双线性对中Frobenius 映射的计算. Costello 等人[15]减少了Ate 双线性对Miller 算法的循环次数, 并运用到高阶扭曲线上进行运算.

幂指数运算(final exponentiation, FinalExp) 是双线性对运算中另一个耗时的操作. Devegili 等人[16]优化了BN 曲线上的FinalExp 运算并给出了Tate 对和Ate 对的快速实现, 比之前的方法更快速、占用的内存更少. Scott 等人[17]通过分析多种配对友好曲线的结构, 提出了Tate 对及其变体的FinalExp 困难部分的通用实现方法, 比之前的方法更快速、更加通用. Granger 等人[18]提出了域特征满足p ≡1 (mod 6) 的分圆子群中平方运算的快速实现, 大大提高了FinalExp 困难部分的计算效率. Fuentes 等人[19]提出双线性对指数运算后仍是双线性对, 将FinalExp 困难部分的指数替换为另一个容易分解的指数, 从而减少加法链的运算量. Duquesne 等人[20]针对BN 曲线上Tate 对及其变体的FinalExp 困难部分提出了4 种新的计算方法, 与以前的实现方法相比需要的内存资源减少了约37%.

Beuchat 等人[21]设计了BN 曲线上O-ate 对的快速软件实现库, 通过选择BN 曲线的参数来减少Miller 算法和FinalExp 的操作数量, 在Intel Core i7 @2.8 GHz 处理器平台, 计算254 比特BN 曲线下的O-ate 对需要0.832 毫秒. Naehrig 等人[22]提出了有限域元素新的表示方法, 利用AMD64 架构的双精度浮点SIMD 指令在257 比特的BN 曲线上实现了O-ate 对, 在英特尔Core 2 Quad Q6600 处理器上计算一次O-ate 对需要4470 408 个时钟周期. Aranha 等人[23]将延迟约减(lazy reduction) 应用到整个双线性对计算过程, 提出当BN 曲线参数为负数时避免FinalExp 中求逆运算的方法, 在Phenom I 平台计算BN254 曲线下的O-ate 对需要个1562 000 个时钟周期. Azarderakhsh 等人[24]比较了使用仿射坐标和标准射影坐标实现O-ate 对的计算效率, 并在多个平台实现了多个安全等级BN 曲线下的O-ate对, 在x86-64 AMD Opteron II @2.4 GHz 处理器平台, 使用C 语言和标准射影坐标计算BN254 曲线下的O-ate 对需要3 290 000 个时钟周期. 针对SM9 算法双线性对, Zhen 等人[25]分析了SM9 双线性对的计算过程和相应的优化方法, 将Miller 循环和FinalExp 的效率分别提高了约5.2% 和0.91%. Cheng等人[26]基于SM9 算法参数对R-ate 双线性对进行了优化, 并通过Frobenius 映射来降低硬件成本, 基于C++ 验证了优化算法的有效性, 并基于FPGA 提出了硬件并行设计.

本文工作. 本文结合当前双线性对的优化实现方法, 提出了SM9 算法双线性对的快速实现方法. 理论分析显示, 本方法的计算复杂度低于现有的实现方法. 实验结果显示, 在Intel(R) Core(TM) i7-6500U@2.50 GHz 处理器上, 本方法计算一次SM9 算法双线性对的时间为3.389 毫秒.

2.1 符号定义

表1 给出了文中使用符号的定义.

表1 符号定义Table 1 Notations and their definitions

2.2 BN 曲线

根据文献[11], BN 曲线E在有限域Fp上点群E(Fp) 的阶为r= #E(Fp),r是一个素数. 基域特征p, 群的阶r和Frobenius 迹tr都由参数t定义:

其中t可以是满足p(t) 和r(t) 都为素数的任意整数. 根据《SM9 标识密码算法参数定义》, SM9 算法使用BN 曲线, 参数t=0x600000000058F98A,p和r为256 比特长的素数. 由于BN 曲线的嵌入度为12,SM9 算法双线性对需要在有限扩域Fp12中进行计算.

2.3 R-ate 对

算法1 R-ate 对),s = 6t+2 Output: Ra(Q,P)1 设s = ∑L-1 i=0 si2i, sL-1 = 1, si ∈{0,1};Input: P ∈E(Fp), Q ∈E′(Fp2 2 初始化T ←Q,f ←1;3 for i from L-2 to 0 do 4 计算f ←f2 ·gT,T (P); T ←[2]T;5 if si = 1 then f ←f ·gT,Q(P); T ←T +Q;7 end 8 end 9 计算Q1 ←πp(Q), Q2 ←πp2 (Q);10 计算f ←f ·gT,Q1 (P); T ←T +Q1;11 计算f ←f ·gT,-Q2 (P); T ←T -Q2;12 计算f ←fp12-1 6 r ;13 输出f.

3.1 塔式扩张构建方法

塔式扩张是R-ate 对运算的基础, 根据《SM9 标识密码算法参数定义》[2], Fp12采用1-2-4-12 的塔式扩张方式构建, 即:

定理1 1-2-4-12 扩张方式和1-2-6-12 扩张方式可以相互转换.

证明: 设f是扩域Fp12的元素. 根据1-2-4-12 的扩张方式, 假设f=a+bw+cw2=(a0+a1v)+(b0+b1v)w+(c0+c1v)w2=a0+b0w+c0w2+a1w3+b1w4+c1w5. 根据1-2-6-12 的扩张方式, 假设f=g+ht= (g0+g1s+g2s2)+(h0+h1s+h2s2)t=g0+h0t+g1t2+h1t3+g2t4+h2t5. 根据两种扩张方式的二次扩域构建是相同的, 有w6=t6=u, 且a0+b0w+c0w2+a1w3+b1w4+c1w5=g0+h0t+g1t2+h1t3+g2t4+h2t5, 因此有各项系数对应相等, 得到系数转换如图1 所示. 同理, 也能得到1-2-6-12 扩张到1-2-4-12 扩张的转换.

图1 1-2-4-12 扩张到1-2-6-12 扩张的转换Figure 1 Conversion from 1-2-4-12 to 1-2-6-12 extension

可以发现, 两种扩张方式的转化是没有开销的, 因此我们可以利用扩域Fp6中的快速平方和求逆来加速最后幂运算中分圆域Gφ6(Fp2) 的运算, 文献[18] 给出了具体的算法.

3.2 优化平方算法

本文采用文献 [18] 的方法来实现扩域 Fp2的平方运算, 假设a=a0+a1u ∈Fp2, 有a2= (a0+βa1)(a0+a1)-a0a1(1 +β) + 2a0a1u. 类似地, 该方法也可用于扩域Fp4的平方运算. 本文将文献[27] 的SQR3 方法用于扩域Fp12元素的平方运算, 如算法2 所示, 该算法需要4 次Fp4平方、1 次Fp4乘法和一些加法运算. 表2 总结了基域及各有限扩域中基础运算的计算开销, 在实现Fp12平方运算时, 本文的方法需要11 个Fp2域上的乘法, 比文献[21,23,24] 的方法少一个.

算法2 扩域Fp12 的平方运算Input: f = f0 +f1w+f2w2 ∈Fp12 Output: h = f2 = h0 +h1w+h2w2, 其中h0 = f20 +2f1f2v, h1 = f22 v+2f0f1, h2 = f21 +2f0f2 1 h0 ←f20;2 h1 ←f22;3 s0 ←f2 +f0;4 s1 ←(s0 -f1)2;5 s0 ←(s0 +f1)2;6 s2 ←f1f2;7 s2 ←2s2;8 s3 ← s0+s1 2 ;9 h2 ←s3 -h1 -h0;10 h1 ←h1v+s0 -s2 -s3;11 h0 ←h0 +s2v;12 输出h = h0 +h1w+h2w2.

表2 基域和有限扩域的计算开销Table 2 Computational cost of based field and finite extension fields

当x1/=x2时, 设gT,Q是穿过T和Q的直线, 则gT,Q=y-mx+mx1-y1. 因此gT,Q在点P(xP,yP)∈E(Fp):y2=x3+b(b/=0) 的值为

当x1=x2时, 类似地, 设gT,T是过T点的切线, 其在点P(xP,yP) 的值为

对于六次乘扭曲线, 线函数在P点的值为g= ˜g0+ ˜g2w2+ ˜g3w3稀疏元素的形式. 对于f=f0+f1w+f2w2,fi ∈Fp4,g= ˜g0+˜g2w2+˜g3w3=g0+˜g2w2,˜gi ∈Fp2, 设h=f ·g, 则

算法3 给出了乘扭曲线下用稀疏乘法计算f ·g的算法描述.

算法3 乘扭曲线稀疏乘法Input: f = f0 +f1w+f2w2,g = ˜g0 + ˜g2w2 + ˜g3w3 = g0 + ˜g2w2 Output: h = f ·g = h0 +h1w+h2w2 1 t0 ←f0 ·g0;2 t1 ←Fp4SparseMul(f2,˜g2);3 u0 ←Fp4SparseMul(f1 +f2,˜g2);4 u1 ←(f0 +f2)·[(˜g0 + ˜g2)+ ˜g3v];5 u2 ←(f0 +f1)·g0;6 h0 ←t0 +(u0 -t1)v;7 h1 ←u2 -t0 +t1v;8 h2 ←u1 -t0 -t1;9 输出h = h0 +h1w+h2w2.

类似地, 对于六次除扭曲线, 线函数在P点的值为g= ˜g0+˜g1w+˜g3w3稀疏元素的形式[24]. 对于f=f0+f1w+f2w2,fi ∈Fp4,g= ˜g0+˜g1w+˜g3w3=g0+˜g1w,˜gi ∈Fp2, 设h=f ·g, 则

算法4 给出了除扭曲线下用稀疏乘法计算f ·g的算法描述.

算法4 除扭曲线稀疏乘法Input: f = f0 +f1w+f2w2,g = ˜g0 + ˜g1w+ ˜g3w3 = g0 + ˜g1w Output: h = f ·g = h0 +h1w+h2w2 1 t0 ←f1 ·g0;2 t1 ←Fp4SparseMul(f2,˜g1);3 u0 ←Fp4SparseMul(f0 +f2,˜g1);4 u1 ←(f1 +f2)·[(˜g0 + ˜g1)+ ˜g3v];5 u2 ←(f0 +f1)·g0;6 h0 ←u2 -t0 +t1v;7 h1 ←u0 +t0 -t1;8 h2 ←u1 -t0 -t1;9 输出h = h0 +h1w+h2w2.

算法3 和算法4 都调用了函数Fp4SparseMul, 将一个稀疏的Fp4元素(即Fp2元素) 与一个Fp4元素相乘, 具体如算法5 所示. 算法3 和4 需执行3 次Fp4乘法、2 次Fp4SparseMul、9 次Fp4加法和1 次Fp2加法,根据表2,一次稀疏乘法的计算开销为3·(3 ˜m+5˜a+mξ)+2·2 ˜m+9·2˜a+˜a=13 ˜m+34˜a+3mξ.

算法5 Fp4SparseMul Input: a = a0 +a1v ∈Fp4,b0 ∈Fp2 Output: c = a·b0 = c0 +c1v 1 c0 ←a0 ·b0;2 c1 ←a1 ·b0;3 输出c = c0 +c1v.

5.1 基于NAF 的点乘运算优化实现

因此对算法1 的第3 步改进如下, 将s表示为2-NAF 形式, 从次高位至低位扫描每一位si. 每次计算点倍T= [2]T, 求线函数值, 并计算f2·gT,T(P); 若si= 1, 则计算点加T+Q, 求线函数值, 并计算f ·gT,Q(P); 若si=¯1, 则计算点加T+(-Q), 求线函数值, 并计算f ·gT,-Q(P). 为此, 我们需要预先计算-Q, 该操作只需要Fp2上的取负. 改进的双线性计算如算法6 所示. 原始的s比特长度为66, 汉明重量为16, 2-NAF 形式的s比特长度为66, 汉明重量为11, 因此将s表示为2-NAF 形式可以减少5 次点加运算、线函数求值和稀疏乘法.

5.2 Frobenius 映射优化实现

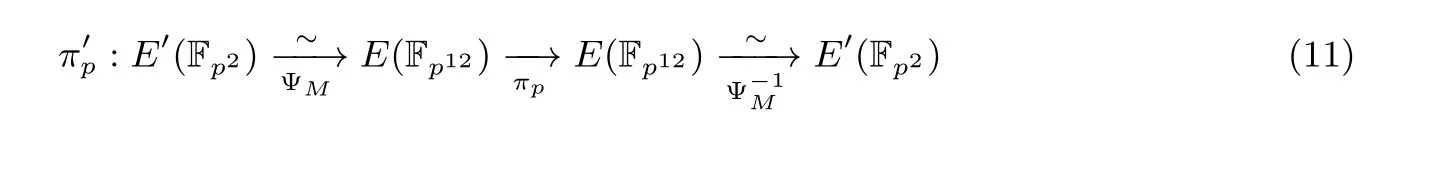
算法6 改进的R-ate 对Input: P ∈E(Fp), Q ∈E′(Fp2),s = 6t+2 Output: Ra(Q,P)1 设s = ∑L-1 i=0 si2i, sL-1 = 1, si ∈{¯1,0,1};2 初始化T ←Q,f ←1;3 for i from L-2 to 0 do f ←f ·gT,Q(P); T ←T +Q;7 end 8 else if si = ¯1 then 4 计算f ←f2 ·gT,T (P); T ←[2]T;5 if si = 1 then 6 f ←f ·gT,-Q(P); T ←T -Q;10 end 11 end 12 计算Q1 ←πp(Q), Q2 ←πp2 (Q);13 计算f ←f ·gT,Q1 (P); T ←T +Q1;14 计算f ←f ·gT,-Q2 (P); T ←T -Q2;15 计算f ←fp12-1 9 r ;16 输出f.

5.3 Miller 算法计算复杂度分析

根据文献[24], 我们使用标准射影坐标计算点运算和线函数, 使用该坐标系, 一次点倍及线函数求值的计算开销为2 ˜m+7˜s+22˜a+4m, 一次点加及线函数求值的计算开销为11 ˜m+2˜s+8˜a+4m. 通过以上的优化, Miller 算法中一共需要执行65 次Fp12平方、点倍及线函数求值、稀疏乘法, 12 次点加及线函数求值、稀疏乘法,2 次Frobenius 映射. 根据表2,Miller 算法的计算开销为65·[(11 ˜m+43˜a+11mξ)+(2 ˜m+7˜s+22˜a+4m)+(13 ˜m+34˜a+3mξ)]+12·[(11 ˜m+2˜s+8˜a+4m)+(13 ˜m+34˜a+3mξ)]+2·(2a+4m)=1978 ˜m+479˜s+6939˜a+312m+946mξ+4a.

根据文献[21,29],FinalExp 中3 次指数为t的模幂运算约占FinalExp 运算时间的79%,而FinalExp约占整个双线性对计算时间的42%. 因此, 优化幂指数运算可以有效提高R-ate 对的性能.

6.1 基于NAF 的幂指数优化实现

2-NAF 形式的t比特长度为63, 汉明重量减少为11, 从而在一次计算mt时, 可以减少3 次扩域Fp12乘法运算.

我们采用文献[29] 提出的压缩平方算法来提高平方运算的效率. 对于g=(g0+g1v)+(g2+g3v)w+(g4+g5v)w2∈Gφ6(Fp2), 压缩函数C和解压缩函数D定义如下[29]:

其中,

若h=g2=(h0+h1v)+(h2+h3v)w+(h4+h5v)w2, 那么有D(g2)=[h2,h3,h4,h5], 根据文献[29] 的SQR2345, 其中

根据Karatsuba 乘法[30], 6g4g5=3·[(g4+g5)2-g24-g25], 6g2g3=3·[(g2+g3)2-g22-g23]. 因此解压缩函数的计算开销是3˜s+2 ˜m+˜i+9˜a+2mξ, 压缩乘法的计算开销是6˜s+28˜a+3mξ.

改进的模幂运算如算法7 所示, 利用Montgomery 同时求逆方法[24], 指数为t的幂指数运算的计算开销为62·(6˜s+28˜a+3mξ)+10·(18 ˜m+60˜a+8mξ)+11·(3 ˜m+3˜s+9˜a+2mξ)+3·10 ˜m+˜i= 243 ˜m+ 405˜s+˜i+ 2435˜a+ 288mξ. 若不采用压缩平方, 指数为t的幂指数运算的计算开销为62·(6 ˜m+37˜a+7mξ)+10·(18 ˜m+60˜a+8mξ)+3˜a=552 ˜m+2897˜a+514mξ, 因此采用压缩平方算法能够减少约6.8% Fp上的乘法和约16% Fp上的加法运算.

算法7 基于2-NAF 的模幂运算Input: m,m-1,t = ∑l-1 i=0 ti2i,ti ∈{¯1,0,1},tl-1 = 1 Output: c = mt 1 初始化c ←t;2 for i from L-2 to 0 do 3 计算c ←c2;4 if si = 1 then c ←c·m;6 end 7 else if si = ¯1 then 5 c ←c·m-1;9 end 10 end 11 输出c.8

6.2 FinalExp 计算复杂度分析

对于简单部分,fp6-1= ¯f · f-1[21], 因此需要一次共轭、一次求逆和一次乘法, 计算开销为3˜a+(25 ˜m+9˜s+˜i+61˜a+12mξ)+(18 ˜m+60˜a+8mξ)=43 ˜m+9˜s+˜i+124˜a+20mξ; 计算fp2+1, 需要一次p2次的Frobenius 映射和一次乘法, 计算开销为5·2m+(18 ˜m+60˜a+8mξ)=18 ˜m+60˜a+10m+8mξ.

通过以上优化, 对于困难部分, 需要计算ft,ft2,ft3,fp,fp2,fp3,(ft)p,(ft2)p,(ft3)p,(ft2)p2, 这10个值的计算开销是3 次指数为t的模幂运算、4 次p次Frobenius 映射和3 次p2次Frobenius 映射,即3·(243 ˜m+405˜s+˜i+2435˜a+288mξ)+4·(10m+6a)+3·10m= 729 ˜m+1215˜s+3˜i+7305˜a+70m+864mξ+24a. 然后我们使用文献[17] 的方法, 即加法链, 来计算FinalExp 的困难部分, 计算开销为258 ˜m+943˜a+132mξ. 困难部分的计算开销为987 ˜m+1215˜s+3˜i+8248˜a+70m+996mξ+24a.

因此, FinalExp 的计算开销为1048 ˜m+1224˜s+4˜i+8432˜a+80m+1024mξ+24a.

本节针对所提出的R-ate 对快速实现方法进行性能评估. 根据前文的分析, 表3 中总结了R-ate 对所需的计算开销. 进一步地, 为了直观地说明计算R-ate 对需要的运算数量, 我们将表3 中扩域Fp2的运算用基域Fp的乘法和加法运算表示. 依据《SM9 标识密码算法参数定义》, 本文使用R-ate 对作为SM9算法双线性对的实例. 由于R-ate 对的实现文献较少, 考虑到O-ate 对与R-ate 对算法类似, 我们将本文的优化实现方法用于O-ate 对, 并与O-ate 对的经典实现方法进行对比, 结果如表4 所示.

表3 R-ate 对所需的运算数量Table 3 Operation counts for R-ate pairing computation

表4 双线性对实现所需的运算数量比较Table 4 Comparison of operation counts for pairing implementation

实现O-ate 对时, Miller 算法所需的Fp乘法数量比文献[21,23,24] 更少, 比文献[21] 和[24] 分别减少了约6.9% 和4.6%; FinalExp 所需的乘法数量比文献[21] 减少了约18.6%, 但比文献[23,24] 多, 这是由于文献[23,24] 使用了文献[19] 的技巧来优化FinalExp, 使用另一个易于分解的指数来简化加法链. 文献[19] 保持了双线性对的双线性性质, 但改变了其运算结果. 本文严格遵循《SM9 标识密码算法》[2]中双线性对的参数选取, 为保证计算结果与标准示例的一致性, 未采用该方法进行优化.

本文测试程序的构建基于密码开源库RELIC 0.5.0[31], 依据《SM9 标识密码算法参数定义》使用C语言进行实现. 测试环境为一台配置有64 位Windows 10 操作系统, Intel(R) Core(TM) i7-6500U CPU@2.50 GHz, 8.00 GB RAM 的惠普笔记本电脑. 取500 次实验运行时间的平均值作为测试结果, 如表5 所示, 结果显示本实现计算一次R-ate 对需要的时间为3.389 毫秒.

表5 R-ate 对实现性能测试Table 5 Test on efficiency of R-ate pairing

双线性对的计算效率对实现基于双线性对的密码协议具有非常重要的影响, 本文通过详细分析SM9算法R-ate 对的Miller 算法和幂指数运算中的耗时操作, 提出了R-ate 对的一系列优化算法, 包括优化的十二次扩域平方算法、稀疏乘法、基于NAF 的点乘运算优化实现、基于NAF 和加法链的幂指数优化实现. 通过与现有实现方法的对比分析, 本方法在计算复杂度方面具有较高的优势. 实验结果显示, 本实现计算一次R-ate 对需要的时间为3.389 毫秒.

猜你喜欢幂指数乘法运算算乘法小学生学习指导(低年级)(2022年10期)2022-11-05重视运算与推理，解决数列求和题中学生数理化(高中版.高考数学)(2022年1期)2022-04-26部分相干幂指数相位涡旋光束的传输特性研究*物理学报(2022年1期)2022-01-19我们一起来学习“乘法的初步认识”数学小灵通(1-2年级)(2021年10期)2021-11-05《数学通报》2235问题的推广中学数学研究(江西)(2021年6期)2021-06-07《整式的乘法与因式分解》巩固练习语数外学习·初中版(2020年11期)2020-09-10有趣的运算数学小灵通(1-2年级)(2020年6期)2020-06-24把加法变成乘法小学生学习指导(低年级)(2019年9期)2019-09-25基于逼近理想点幂指数评估的防空导弹型谱分析与研究军事运筹与系统工程(2017年1期)2017-07-31“整式的乘法与因式分解”知识归纳中学生数理化·八年级数学人教版(2017年2期)2017-03-25